ウォール街のランダムウォーカーが主張する長期投資によるリスク低減効果は正しいのか

ウォール街のランダムウォーカーは私の投資戦略のバイブルです。以前書いたとおり、人生で初めて読んだ投資関連の本がこれで、最初に買ったのは11版でした。最近13版が出ました。もちろん12, 13版も買っています。

ただ、この本の内容の核心とも言える箇所のひとつに関して、その正しさを問う山崎元さんの記事がありました（こちら）。 この記事の主張をちゃんと理解するために自分で手を動かしてみました。

ところで、実はこれは2年前にFacebookに投稿したものです。やっとブログに成仏させます。かなり熟成が進んでしまっていますが（そもそも↑の山崎さんの記事が書かれたのが2013年）、最近ウォール街のランダムウォーカーが50周年で新版が出たり、日本では来年から新NISAが始まるタイミングだったりでちょうど良いだろうとこじつけます。

また、この文章の内容を包含しつつより幅広い視点で考察されているブログ記事をあとから見つけました→「長期投資はリスクを下げる」は正しいだろうか？平均回帰性のウソとホント。 私の文章は、この記事の補足として、数式的に理解したいときに読むのがいい気がします。

以下本文。

本文: ウォール街のランダムウォーカーが主張する長期投資によるリスク低減効果は正しいのか

私の大好きなマルキール本の誤りが指摘されていたので調べてみた。 曰く、

この本の内容には、一つ深刻な間違いがあると思っている。（…中略…）

長期間投資することによってリスクが縮小するので、投資を考える上では期間が重要だと説明されている。（…中略…）

ところが、この説明は間違いなのだ。

（2013年の記事ですが）https://media.rakuten-sec.net/articles/-/4023

マルキール本は、投資期間中の「年平均リターン」を取り上げて、投資期間が長くなると年平均リターンのちらばりが小さくなる、と主張する¹。

これはおそらく以下のようにかみ砕ける。

あるアセットに投資した際のリターンを計測するにあたって、各年のリターンはある確率分布に従い、投資期間N年間の間、1年ごとにリターンが独立に実現する（i.i.d.）、とモデル化できる。 i年目のリターンの実現値（標本）をx_iとする。 中心極限定理により、このとき、投資期間N年中の各年のリターンの平均値E(x_i)の標準偏差は、Nを大きくすると小さくなる。

中心極限定理: 母分散σ^2のとき、標本数Nの標本平均の分散はσ^2/N。 したがって、「N年間中の年リターンの平均の標準偏差」は「ある年の年リターンの標準偏差」の1/√N倍になる。

これを以って「長期投資はリスクを軽減する」と主張される。

しかし、これは誤謬であり、 投資家が気にするべきなのは各年のリターンの平均値E(x_i)などではなく、 累積のリターン、つまり R(N) = (1 + x_1)(1 + x_2)…(1 + x_N) - 1 であり、 この確率変数の分散はNを大きくしても小さくならない（むしろ、当然ながら、大きくなる）。

マルキール本は、投資家にとって本質的に意味のない「年平均リターン」なる数値を持ち出して、その標準偏差をリスクと呼んで議論したところが不誠実だということになる。

さて、実際にどんな風になるのかやってみた。

以下のリスク資産に投資し、持ち続ける場合を考える。

• 年リターンは正規分布に従う
• 年リターンの期待値4%
• 年リターンの標準偏差15%

この投資を行った際の実現値を100000件シミュレーションし、その統計値を求めた。

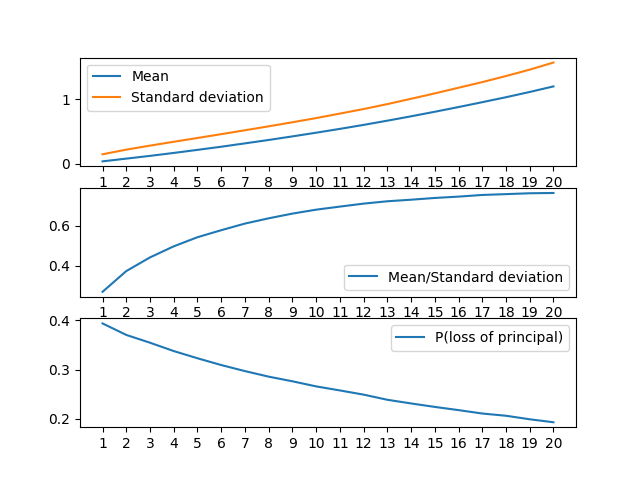
1つ目の図は、以下の値のプロット。横軸は投資期間（年）（以下同じ）。

• n年経過時の最終リターンR(n)の平均 E(R)
• n年経過時の最終リターンR(n)の標準偏差（リスク）σ(R)

投資期間を長く取るほど、リスクもリターンも上がるという主張通りの結果になった。

考えてみれば当然の結果で、 直感的には、「資産をリスクにさらしている時間が伸びるほど、リスクの合計値は大きくなり、取ったリスクに対するリターンも増える」と理解される。

2つ目の図は、E/σの値のプロット。 これはシャープレシオのようなもの。のようなもの、というのは、ここでは無リスク資産のリターンを考えていないから。 シャープレシオは投資期間が伸びるほど高くなっており、「投資期間が伸びるほど投資効率が上がる（リターンに対して相対的にリスクは下がる）」という主張はできそう。ハッピー！

ちなみに3個目の図は元本割れの確率。 投資期間を長く取るほど元本割れはしにくくなる。 （一般的な定義ではなく）元本割れの確率をリスクとして考えるなら、「長期投資はリスクを下げる」は正しい…が、長期に渡り資産をリスクに晒しておいて「元本割れしなければ良い」とはならないだろうから、この図の結果には意味がない。

これは上記記事でも書かれている。

運用期間がより長期間になると運用資産が元本割れする確率は小さくなる。しかし、運用期間が長くなるとそれだけ期待する運用資産の増加も大きいはずだから、「元本割れしないからいい」とはいえないはずだ。

長期投資でシャープレシオが上がる、という結果もなんか都合がいい気がする。時間割引率を導入したら、シャープレシオが上がらない結果も導けそう（そのように割引率を設定できそう）だが、それはそれでいいのか？

しかし、ずっと前から公開されている内容ですが、自分で手を動かしてみると理解が進みますね。 …と言いつつ、統計も経済も素人なので全然自信がありません。 この辺りに詳しい方、ツッコミを頂けると嬉しいです🙇‍♂️

実験のソースコードはこちら： calc.py